Hi there! I joined Lawrence Berkeley National Laboratory in August 2022 as a postdoc, working under the supervision of Dr Chao Yang. Prior to that, I obtained my PhD from Purdue University, where I was advised by Professor Haizhao Yang. Before my doctoral studies, I earned my MSc degree from the National University of Singapore and my BSc from Sun Yat-sen University.
Research Interest: Scientific machine learning, deep learning algorithm and interdisciplinary application.
Contact: senweiliang [at] lbl [dot] gov
News
- [🔝] I am currently exploring new faculty position opportunities. I would greatly appreciate any recommendations or referrals you might be able to provide. Thank you.
- [10/10/2024] 🚀 AlterSGD has been accepted by Multimedia Modeling 2025. Many thanks to all the collaborators for their efforts!
- [09/30/2024] 🚀 AI-driven VQE has been accepted by Chemical Physics Reviews. Many thanks to all the collaborators for their efforts!
- [09/29/2024] 🚀 The journal extension of DIA has been accepted by Neurocomputing. Many thanks to all the collaborators for their efforts!
Awards
- Travel Award, 2024 SIAM Northern and Central California Sectional Meeting
- Travel Award, 2023 International Congress on Industrial and Applied Mathematics
- CVPR Outstanding Reviewer Link.
- Ross-Lynn fellowship, Purdue University, 2021-2022.
- Top Graduate Tutors for AY2019/20, Department of Mathematics, NUS.
- 2020 Thirty-fourth AAAI Conference Scholarship.
Positions
- Postdoc at Lawrence Berkeley National Laboratory, from Aug 2022 to present.
- Wallace Givens Associate at Argonne National Laboratory mentored by Dr. Hong Zhang, from May 2021 to Jul 2021.
- Research Assistant at Computational Medical Imaging Laboratory mentored by Prof. Yao Lu, from Jun 2016 to Jan 2017.
Academic Service
- Conference reviewer: AAAI, CVPR, ECCV, ICCV, ICANN, NeurIPS
- Journal reviewer: Journal of Scientific Computing, Journal of Vibration and Control
- Organizer: AMS Sectional meeting at Purdue, the SIAM Texas-Louisiana Section
Selected publications
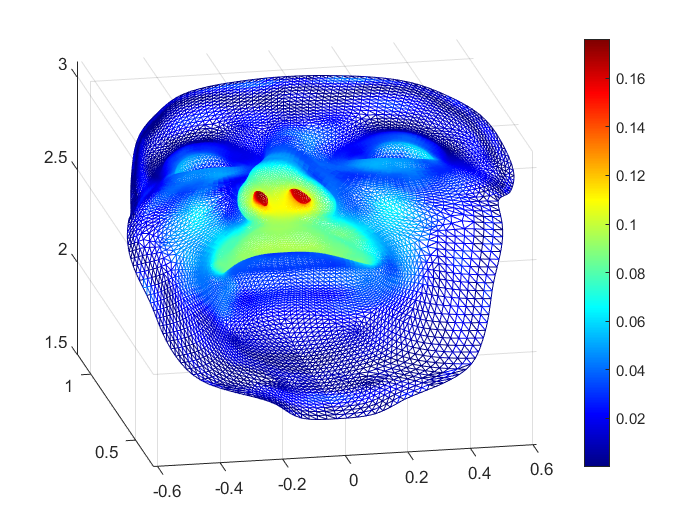
Solving PDEs on unknown manifolds with machine learning
We propose mesh-free deep learning method and theory based on diffusion maps for solving elliptic PDEs on unknown manifolds, identified with point clouds.
S Liang, S Jiang, J Harlim, H Yang, Applied and Computational Harmonic Analysis, Volume 71, 101652, 2024 [PDF Code].
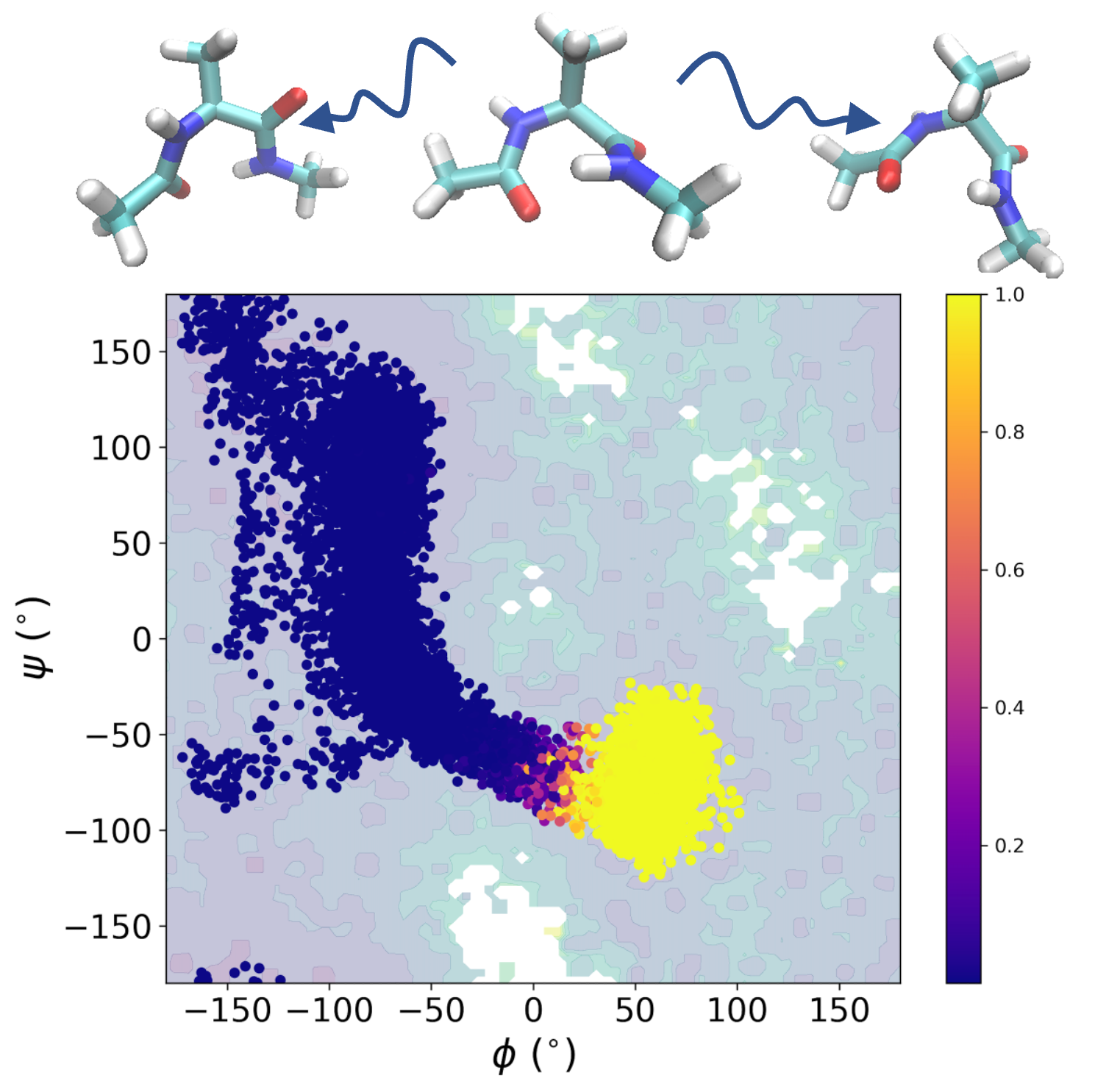
Probing reaction channels via reinforcement learning
We propose deep learning framework to study rare transition including using reinforcement learning to identify reactive regions and employing NN-based PDE solver to approximate the committor function.
S Liang, AN Singh, Y Zhu, DT Limmer, C Yang, Machine Learning: Science and Technology 4 (4) 2023 [PDF, Code].
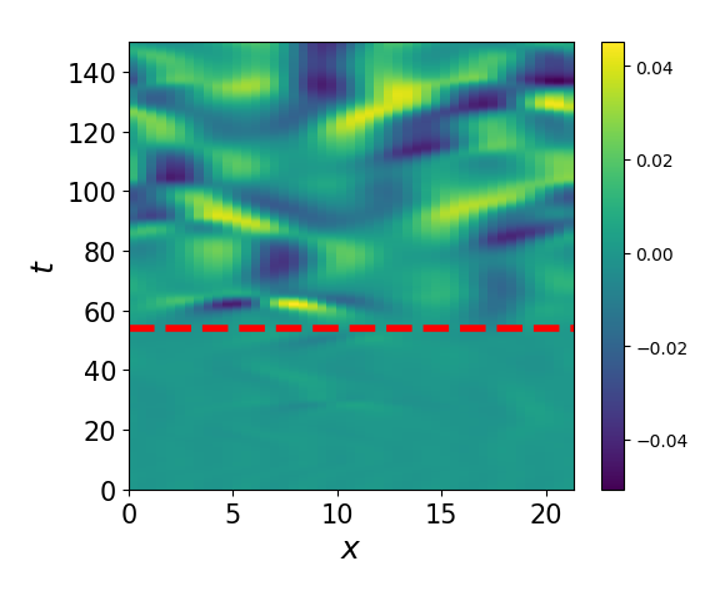
Machine learning for prediction with missing dynamics
We developed a deep learning method to recover missing dynamics resulting from partial understanding or observation of physical processes and the computational expense of numerical simulations.
J Harlim, S Jiang, S Liang, H Yang, Journal of Computational Physics 428, 109922, 2021 [PDF, Code].
Selected manuscripts
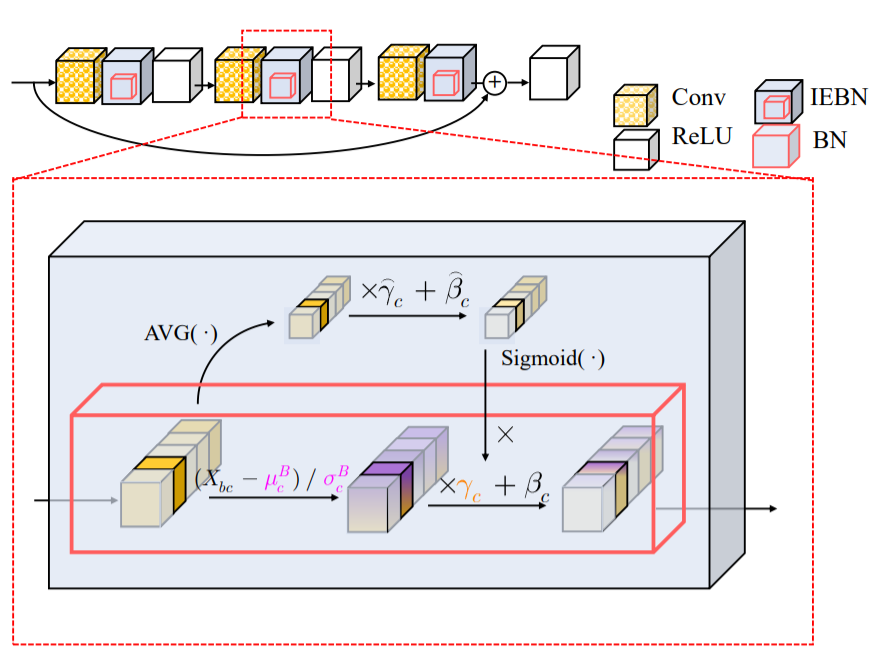
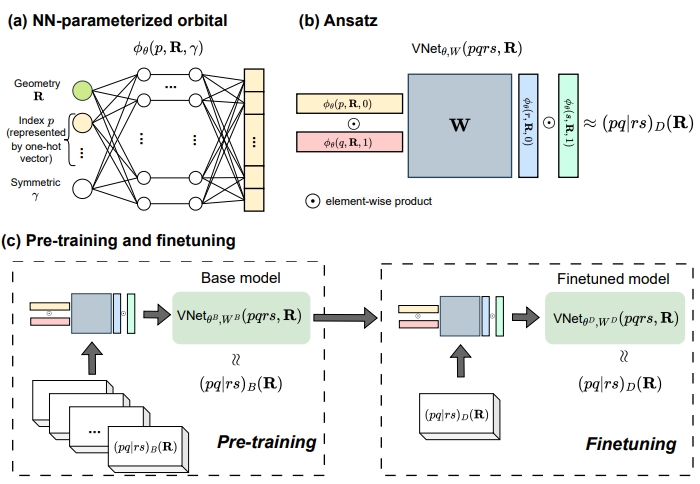
Effective many-body interactions in reduced-dimensionality spaces through neural networks
We introduce a new paradigm to learn the effective Hamiltonian in data-limited scenario.
S Liang, K Kowalski, C Yang and NP Bauman, arXiv:2407.05536 [PDF].
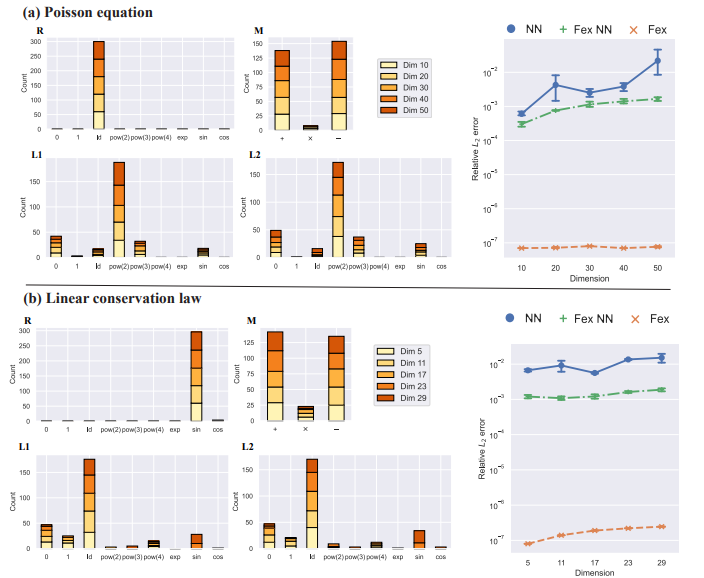
Finite expression method for solving high-dimensional partial differential equations
We introduce a sympolic approach for high dimensional PDE that seeks an approximate PDE solution in the space of functions with finitely many analytic expressions and, hence, this methodology is named the finite expression method (FEX).
This page has been accessed at least
times since 10/10/2021, and on average
per day.